Straty energii hydraulicznej wskutek tarcia
Darcy i Weisbach zastosowali zasadę zachowania masy do objętości płynu pomiędzy dwoma przekrojami prostopadłymi do osi rury, co pozwoliło im na wyprowadzenie następującego równania dla ustalonych przepływów nieściśliwych:
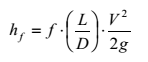
gdzie:
f – współczynnik tarcia – wartość bezwymiarowa,
L – długość rury w m,
D – średnica rury w m,
V – prędkość średnia w m/s,
g – przyspieszenie ziemskie (9,81 m/s2).
W przypadku przepływu laminarnego wartość f może zostać wyliczona bezpośrednio z równania:
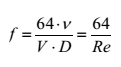
Z równania powyższego wynika, że dla przepływu laminarnego współczynnik tarcia „f” jest niezależny od chropowatości ścianek oraz odwrotnie proporcjonalny do liczby Reynoldsa (Re). Fakt, że wzrost liczby Reynoldsa powoduje spadek współczynnika tarcia, nie oznacza jednak, iż zwiększając prędkość przepływu zmniejszamy straty tarcia.
Podstawiając za f w równaniu wartość współczynnika tarcia z równania , otrzymujemy:
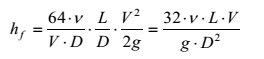
Widać stąd, że w przypadku przepływu laminarnego strata jednostkowej energii hydraulicznej jest wprost proporcjonalna do Vi odwrotnie proporcjonalna do D2. Kiedy przepływ jest praktycznie turbulentny (Re>2000), współczynnik tarcia staje się słabiej zależny od liczby Reynoldsa i bardziej zależny od względnej wysokości chropowatości e/D, gdzie „e” reprezentuje średnią wysokość nieregularności na ściankach rury, a D jest średnicą rury. Niektóre wartości parametru chropowatości e przedstawiono w tabeli:
Tabela: Wartość chropowatości e dla różnych materiałów rur
Wiadomo, że nawet w przepływie turbulentnym tuż przy ściance rury istnieje bardzo cienka warstwa cieczy płynącej w sposób uporządkowany, zwana podwarstwą laminarną. Kiedy rośnie wartość Re, zmniejsza się grubość tej podwarstwy. Jeśli tylko wartość parametru chropowatości e jest zdecydowanie mniejsza niż grubość podwarstwy, rura jest uznawana za hydraulicznie gładką.
W hydraulicznie gładkiej rurze chropowatość powierzchni nie ma wpływu na współczynnik tarcia f.
Dlatego von Karman wyprowadził dla takiego przypadku następujące równanie:
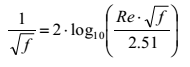
Przy wysokich wartościach liczby Reynoldsa grubość podwarstwy staje się bardzo mała, a zależność współczynnika tarcia od Re ustaje na rzecz zależności od względnej wysokości chropowatości. W tym przypadku rura staje się hydraulicznie chropowata, a współczynnik tarcia opisuje podane przez von Karmana równanie:
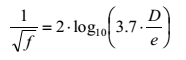
Dla przypadku rury, która nie jest ani gładka ani chropowata, Colebrook i White zaproponowali równanie:
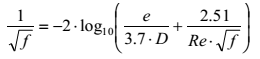
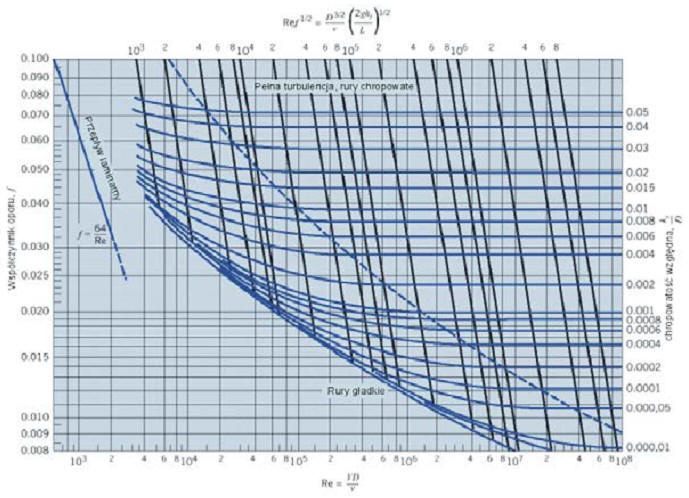
Równanie trudno rozwiązać metodami analitycznymi, co zachęciło Moody’ego do sporządzenia swojego znanego diagramu „współczynników tarcia dla przepływu przez rurę”.
Na podstawie diagramu wyróżnić można cztery różne strefy przepływów:
1. Strefa przepływu laminarnego w którym f jest liniową funkcją Re
2. Niedokładnie określona strefa krytyczna
3. Strefa przejściowa, zaczynająca się na rurach gładkich i kończąca się kreskowaną linią, w której f zależy zarówno od Re jak i e/D
4. Strefa rozwiniętej turbulencji, w której f zależy tylko od e/D
Źródło:
– instsani.pl